Equation
Relativistic Quantum Mechanics: Spin & Dirac Equation eBooks & eLearning
Posted by ELK1nG at Sept. 7, 2022
Relativistic Quantum Mechanics: Spin & Dirac Equation
Published 9/2022
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz
Language: English | Size: 6.01 GB | Duration: 8h 51m
Published 9/2022
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz
Language: English | Size: 6.01 GB | Duration: 8h 51m
Mathematical Intuition behind Relativistic Quantum Mechanics
Linear Equation Part- I Linear Equation In One Variable eBooks & eLearning
Posted by ELK1nG at Sept. 6, 2023
Linear Equation Part- I Linear Equation In One Variable
Published 9/2023
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz
Language: English | Size: 970.09 MB | Duration: 1h 0m
Published 9/2023
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz
Language: English | Size: 970.09 MB | Duration: 1h 0m
Linear Equations in One Variable
Linear Equation Part- 2 Linear Equations In Two Variables eBooks & eLearning
Posted by ELK1nG at Sept. 7, 2023
Linear Equation Part- 2 Linear Equations In Two Variables
Published 9/2023
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz
Language: English | Size: 1.26 GB | Duration: 1h 17m
Published 9/2023
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz
Language: English | Size: 1.26 GB | Duration: 1h 17m
Linear Equations in two Variables
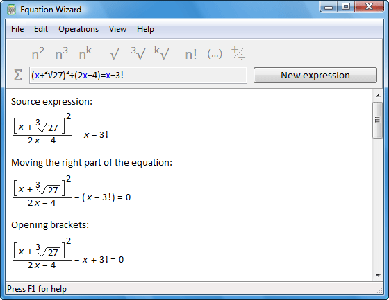
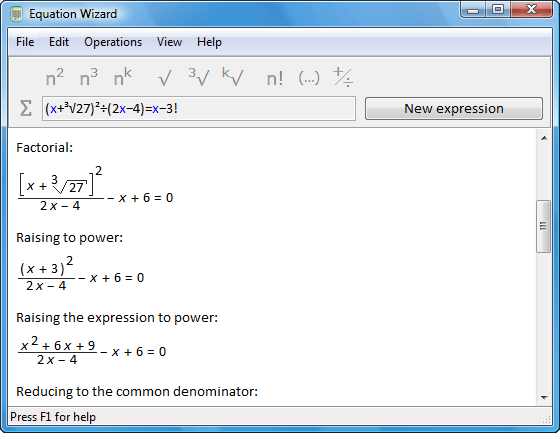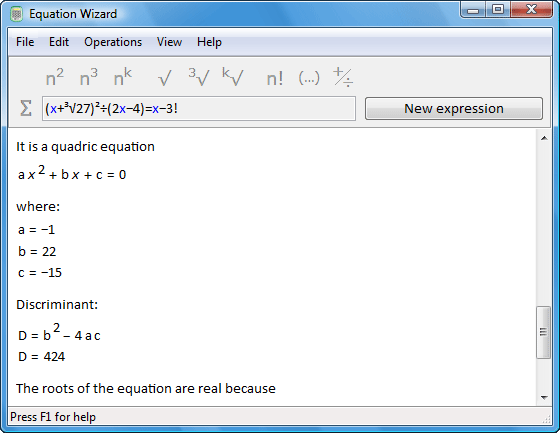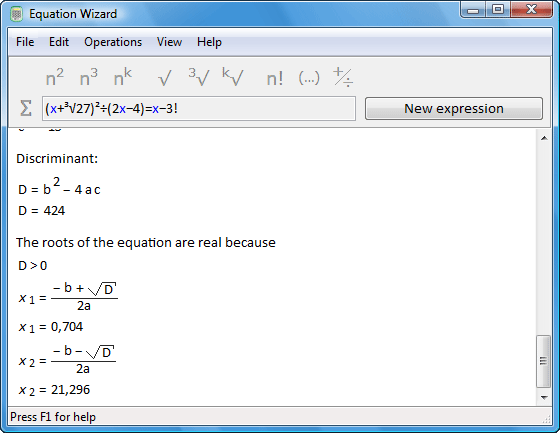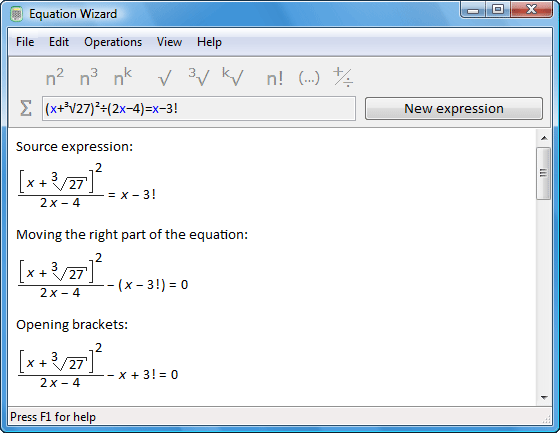
Equation Wizard v1.2 Software
Posted by alone25351 at Sept. 2, 2007
Equation Wizard v1.2 | 1256 KB
Equation Wizard automatically solves algebraic equations written in any form. It means that you do not have to make any preliminary calculations or study the equation. Just type the equation in the program the way you see it in your textbook or notebook. Thanks to its artificial intelligence, the program will analyze the equation and step by step reduce it to a canonical form.
Equation Wizard 1.21 Portable Software
Posted by big1ne at March 25, 2014
Equation Wizard 1.21 Portable | 1.3 MB
Equation Wizard automatically solves algebraic equations written in any form. It means that you do not have to make any preliminary calculations or study the equation. Just type the equation in the program the way you see it in your textbook or notebook. Thanks to its artificial intelligence, the program will analyze the equation and step by step reduce it to a canonical form.
Equation Wizard 1.21 Software
Posted by speedzodiac_ at March 22, 2014
Equation Wizard 1.21 | 1.1 Mb
Equation Wizard automatically solves algebraic equations written in any form. It means that you do not have to make any preliminary calculations or study the equation. Just type the equation in the program the way you see it in your textbook or notebook. Thanks to its artificial intelligence, the program will analyze the equation and step by step reduce it to a canonical form.
Intro To Differential Equation eBooks & eLearning
Posted by IrGens at Feb. 18, 2025
Intro To Differential Equation
.MP4, AVC, 1280x720, 30 fps | English, AAC, 2 Ch | 12h 59m | 6.33 GB
Instructor: Lonzo Fulwider
.MP4, AVC, 1280x720, 30 fps | English, AAC, 2 Ch | 12h 59m | 6.33 GB
Instructor: Lonzo Fulwider
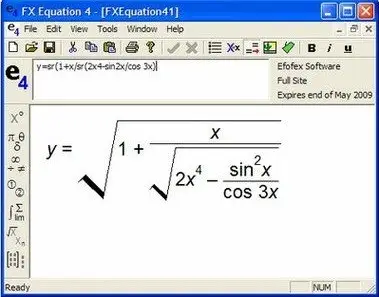
FX Equation 4.004.1 Software
Posted by Dizel_ at Sept. 21, 2010
FX Equation 4.004.1 | 5.48 MB
FX Equation is simply the fastest way to produce mathematical and scientific equations. It provides an equation creation environment that really is "Astoundingly Quick". FX Equation 4 adds automatic vertical alignment of equals signs and a high speed toolbar entry system that can speed up entry of more complicated equations. FX Equation also adds short division signs, "fill in the blank" boxes, combinations, permutations, arcs, highlighted lines and an on-screen keyboard for use with interactive whiteboards. The full list of FX Equation 4 features is listed below.
Quadratic Equation Jee Advanced Pyq (1989-2025) eBooks & eLearning
Posted by ELK1nG at March 14, 2025
Quadratic Equation Jee Advanced Pyq (1989-2025)
Published 3/2025
MP4 | Video: h264, 1920x1080 | Audio: AAC, 44.1 KHz
Language: English | Size: 2.64 GB | Duration: 2h 0m
Published 3/2025
MP4 | Video: h264, 1920x1080 | Audio: AAC, 44.1 KHz
Language: English | Size: 2.64 GB | Duration: 2h 0m
QUADRATIC EQUATION JEE ADVANCED PYQ
Equation - Hazy Daze (1999) Music
Posted by pgf000 at Sept. 9, 2010
Equation - Hazy Daze (1999)
British Folk Rock/Celtic | Putumayo World Music | MP3 CBR 320kbps | 43:47 | 100 MB
Sure, none of your friends have heard of Equation, but they're missing out. I have loved this CD from the very first track and I still can't get enough. Equation's sound has been described as British-Celtic folk-pop. Basically, their sound is all their own and thus this ambiguous description suits them well. They're not quite like anything you've ever heard. But watch out; this album is highly addictive. From the intensely singable "Kissing Crime" to the contemplative "Myself" to the superb "Strange Love," the tracks are all incredibly sincere and beautifully performed. I played this album all summer at the large bookstore where I worked, and every time I played it, someone would come up and ask what was playing. I always highly recommended it to those who asked, as I do to you today. Maybe someday Equation will be the household name that they deserve to be, but for now, they remain one of music's most exquisite hidden treasures. (review from Amazon)