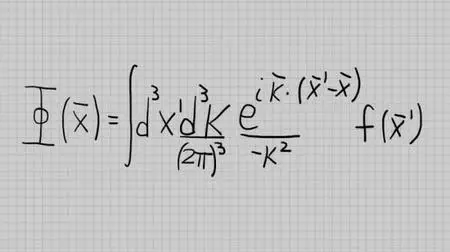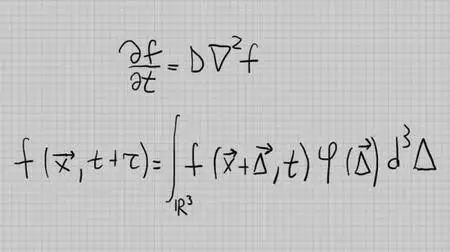Heat Equation
Random Walk and the Heat Equation eBooks & eLearning
Posted by step778 at Aug. 15, 2020
Gregory F. Lawler, "Random Walk and the Heat Equation"
English | 2010 | pages: 170 | ISBN: 0821848291 | PDF | 4,9 mb
English | 2010 | pages: 170 | ISBN: 0821848291 | PDF | 4,9 mb
Random Walk and the Heat Equation eBooks & eLearning
Posted by ksveta6 at Dec. 15, 2015
Random Walk and the Heat Equation by Gregory F. Lawler
2010 | ISBN: 0821848291 | English | 156 pages | PDF | 5 MB
2010 | ISBN: 0821848291 | English | 156 pages | PDF | 5 MB
Partial Differential Equations (Poisson, Laplace, heat eq.) eBooks & eLearning
Posted by ELK1nG at June 9, 2021
Partial Differential Equations (Poisson, Laplace, heat eq.)
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz, 2 Ch
Genre: eLearning | Language: English + srt | Duration: 33 lectures (9h 17m) | Size: 6.8 GB
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz, 2 Ch
Genre: eLearning | Language: English + srt | Duration: 33 lectures (9h 17m) | Size: 6.8 GB
PDE solved by Fourier Transform and the method of separation of variables
The Yang-Mills Heat Equation with Finite Action in Three Dimensions eBooks & eLearning
Posted by readerXXI at March 4, 2023
The Yang-Mills Heat Equation with Finite Action in Three Dimensions
by Leonard Gross
English | 2022 | ISBN: 1470450534 | 124 Pages | True PDF | 1.25 MB
by Leonard Gross
English | 2022 | ISBN: 1470450534 | 124 Pages | True PDF | 1.25 MB
Invariance Theory: The Heat Equation and the Atiyah-Singer Index Theorem eBooks & eLearning
Posted by arundhati at Aug. 29, 2018
Peter B. Gilkey, "Invariance Theory: The Heat Equation and the Atiyah-Singer Index Theorem"
1995 | ISBN-10: 0849378745 | 536 pages | PDF | 21 MB
1995 | ISBN-10: 0849378745 | 536 pages | PDF | 21 MB
Solving the Diffusion/Heat equation by Fourier Tranform eBooks & eLearning
Posted by ELK1nG at June 18, 2021
Solving the Diffusion/Heat equation by Fourier Tranform
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz, 2 Ch
Genre: eLearning | Language: English + srt | Duration: 8 lectures (1h 44m) | Size: 728 MB
MP4 | Video: h264, 1280x720 | Audio: AAC, 44.1 KHz, 2 Ch
Genre: eLearning | Language: English + srt | Duration: 8 lectures (1h 44m) | Size: 728 MB
PDE solved by Fourier Transform (part 2)
Fundamentals Of Heat Transfer Part 1 eBooks & eLearning
Posted by Sigha at Nov. 10, 2023
Fundamentals Of Heat Transfer Part 1
MP4 | Video: h264, 1920x1080 | Audio: AAC, 44.1 KHz
Language: English (US) | Size: 1.98 GB | Duration: 8h 15m
MP4 | Video: h264, 1920x1080 | Audio: AAC, 44.1 KHz
Language: English (US) | Size: 1.98 GB | Duration: 8h 15m
Learn the Fundamentals of Heat Transfer and Thermodynamics: From Conduction to Radiation and Beyond
Geometric Aspects of Partial Differential Equations: Proceedings of a Mininsymposium on Spectral Invariants, Heat Equation Appr eBooks & eLearning
Posted by insetes at April 24, 2022
Geometric Aspects of Partial Differential Equations: Proceedings of a Mininsymposium on Spectral Invariants, Heat Equation Approach, September 18-19, 1998, Roskilde, Denmark By Krzysztof Wojciechowski, Bernhelm Booss-Bavnbek (ed.)
1999 | 282 Pages | ISBN: 0821820613 | DJVU | 3 MB
1999 | 282 Pages | ISBN: 0821820613 | DJVU | 3 MB
Introduction to Partial Differential Equations eBooks & eLearning
Posted by AvaxGenius at July 28, 2020
Introduction to Partial Differential Equations By David Borthwick
English | EPUB | 2016 | 293 Pages | ISBN : 3319489348 | 17.42 MB
This modern take on partial differential equations does not require knowledge beyond vector calculus and linear algebra.
The Index Theorem and the Heat Equation Method (Repost) eBooks & eLearning
Posted by step778 at Nov. 14, 2018
Yanlin Yu, Weiping Zhang, "The Index Theorem and the Heat Equation Method"
2001 | pages: 308 | ISBN: 9810246102 | DJVU | 1,5 mb
2001 | pages: 308 | ISBN: 9810246102 | DJVU | 1,5 mb